|
In the convection
section, heat is transferred by both radiation and convection. The
convection transfer coefficients for fin and stud tubes are explored
here as well as bare tube transfer. The short beam radiation is
treated separately from the convection transfer below.
This section of Fired Heater Design is divided into five main areas,
which can be selected from the subject drop down box above or you
may use the jump links below to go to a section. You may also use
your browser "back button" to return to where you were.
Overall Heat Transfer Coefficient,
Uo:
Uo =
1/Rto
Where,
|
Uo = Overall heat transfer coefficient,
Btu/hr-ft2-F |
|
Rto = Total outside thermal resistance,
hr-ft2-F/Btu |
And,
|
Rto = Ro + Rwo + Rio |
|
Ro = Outside thermal resistance,
hr-ft2-F/Btu |
|
Rwo = Tube wall thermal resistance,
hr-ft2-F/Btu |
|
Rio = Inside thermal resistance,
hr-ft2-F/Btu |
And the resistances are
computed as,
|
Ro = 1/he |
|
Rwo =
(tw/12*kw)(Ao/Aw) |
|
Rio =
((1/hi)+Rfi)(Ao/Ai) |
Where,
|
he = Effective outside heat transfer coefficient,
Btu/hr-ft2-F |
|
hi = Inside film heat transfer coefficient,
Btu/hr-ft2-F |
|
tw = Tubewall thickness, in |
|
kw = Tube wall thermal conductivity, Btu/hr-ft-F |
|
Ao = Outside tube surface area, ft2/ft |
|
Aw = Mean area of tube wall, ft2/ft |
|
Ai = Inside tube surface area, ft2/ft |
|
Rfi = Inside fouling resistance,
hr-ft2-F/Btu |
Inside film heat
transfer coefficient, hi:
The inside heat transfer coefficient
calculation procedure is covered in detail, elsewhere in this
course.
Effective outside heat transfer coefficient, he
he =
1/(1/(hc+hr)+Rfo)
Where,
|
hc = Outside heat transfer coefficient,
Btu/hr-ft2-F |
|
hr = Outside radiation heat transfer coefficient,
Btu/hr-ft2-F |
|
Rfo = Outside fouling resistance,
hr-ft2-F/Btu |
Outside film heat
transfer coefficient, hc:
The bare tube heat transfer film
coefficient, hc, can be described by the following equations.
For
a staggered tube arrangement,
hc =
0.33*kb(12/do)((cp*mb)/kb)1/3((do/12)(Gn/mb)))0.6
And for an
inline tube arrangement,
hc =
0.26*kb(12/do)((cp*mb)/kb)1/3((do/12)(Gn/mb)))0.6
Where,
|
hc = Convection heat transfer coefficient,
Btu/hr-ft2-F |
|
do = Tube outside diameter, in |
|
kb = Gas thermal conductivity, Btu/hr-ft-F |
|
cp = Gas heat capacity, Btu/lb-F |
|
mb = Gas dynamic viscosity,
lb/hr-ft |
|
Gn = Mass velocity of gas,
lb/hr-ft2 |
We can describe a sample bare
tube bank as follows:
|
Process Conditions:
Gas flow, lb/hr = 100,000
Gas
temperature in, °F = 1000
Gas temperature out, °F = 868
Compostion,
moles
N2, % = 71.5779
O2, % =
2.8800
CO2, % = 8.6404
H2O, % = 16.4044
Ar,
% = 0.8609
Mechanical Conditions:
Tube Diameter, in =
4.500
Tube Spacing, in = 8
Number Tubes Wide = 8
Tube Effective
Length, ft = 13.000
Number Of Tubes = 48
Tube Arrangement =
Staggered Pitch
|
 |
Gas Properties
For the gas
properties, we can use the script we used in the radiant section design to get
the properties of the gas at the average temperature.
From
this program, we get the following properties,
kb, Btu/hr-ft-F =
0.0315
cp, Btu/lb-F = 0.2909
mb, cp = 0.0340 = 0.0340*2.42 = 0.0823
lb/hr-ft
To calculate the mass velocity, Gn, we need to first
calculate the net free area of the tube bank. For these calculations, we are
going to assume the tube rows are corbelled, so the net free area, NFA:
NFA =
Nwide*tspc/12*tlgth-Nwide*tOd/12*tlgth
= 8*8/12*13-8*4.5/12*13 = 30.333 ft2
Therefore,
Gn
= Wgas / NFA = 100000/30.333 = 3296.739
And using our formula for
hc,
hc = 0.33*0.0315 (12/4.5)((0.2909
*0.0823 )/0.0315 )1/3((4.5/12)(3296.739/0.0823 )))0.6 =
8.1115
To get a feel for the values of the coeffcient, use
the following script to run various designs.
The radiation transfer coefficient, hr is described later in this
section. Fouling resistances, Rfi and Rfo are allowances
that depend upon the process or service of the heater and the fuels that are
being burned.
Convection Transfer, Fin Tubes
You will notice that the heat transfer equations for the fin tubes are
basically the same as for the bare tubes untill you reach the he
factor, where a new concept is introduced to account for the fin or extended
surface. The procedure presented herein are taken from the Escoa manual which
can be downloaded in full from the internet.
Overall Heat Transfer
Coefficient, Uo:
Uo =
1/Rto
Where,
|
Uo = Overall heat transfer coefficient,
Btu/hr-ft2-F |
|
Rto = Total outside thermal resistance,
hr-ft2-F/Btu |
And,
|
Rto = Ro + Rwo + Rio |
|
Ro = Outside thermal resistance,
hr-ft2-F/Btu |
|
Rwo = Tube wall thermal resistance,
hr-ft2-F/Btu |
|
Rio = Inside thermal resistance,
hr-ft2-F/Btu |
And the resistances are
computed as,
|
Ro = 1/he |
|
Rwo =
(tw/12*kw)(Ao/Aw) |
|
Rio =
((1/hi)+Rfi)(Ao/Ai) |
Where,
|
he = Effective outside heat transfer coefficient,
Btu/hr-ft2-F |
|
hi = Inside film heat transfer coefficient,
Btu/hr-ft2-F |
|
tw = Tubewall thickness, in |
|
kw = Tube wall thermal conductivity, Btu/hr-ft-F |
|
Ao = Total outside surface area, ft2/ft |
|
Aw = Mean area of tube wall, ft2/ft |
|
Ai = Inside tube surface area, ft2/ft |
|
Rfi = Inside fouling resistance,
hr-ft2-F/Btu |
Inside film heat
transfer coefficient, hi:
The inside heat transfer coefficient
calculation procedure is covered in detail, elsewhere in this
course.
Effective outside heat transfer coefficient,
he:
he =
ho(E*Afo+Apo)/Ao
Where,
|
ho = Average outside heat transfer coefficient,
Btu/hr-ft2-F |
|
E = Fin efficiency |
|
Ao = Total outside surface area, ft2/ft |
|
Afo = Fin outside surface area, ft2/ft |
|
Apo = Outside tube surface area,
ft2/ft |
And,
Average outside heat
transfer coefficient, ho:
ho =
1/(1/(hc+hr)+Rfo)
Where,
|
hc = Outside heat transfer coefficient,
Btu/hr-ft2-F |
|
hr = Outside radiation heat transfer coefficient,
Btu/hr-ft2-F |
|
Rfo = Outside fouling resistance,
hr-ft2-F/Btu |
Outside film heat
transfer coefficient, hc:
hc =
j*Gn*cp(kb/(cp*mb))0.67
Where,
|
j = Colburn heat transfer factor |
|
Gn = Mass velocity based on net free area,
lb/hr-ft2 |
|
cp = Heat capacity, Btu/lb-F |
|
kb = Gas thermal conductivity, Btu/hr-ft-F |
|
mb = Gas dynamic viscosity,
lb/hr-ft |
Colburn heat transfer factor,
j:
j =
C1*C3*C5(df/do)0.5((Tb+460)/(Ts+460))0.25
Where,
|
C1 = Reynolds number correction |
|
C3 = Geometry correction |
|
C5 = Non-equilateral & row correction |
|
df = Outside diameter of fin, in |
|
do = Outside diameter of tube, in |
|
Tb = Average gas temperature, F |
|
Ts = Average fin temperature,
F |
Reynolds number correction,
C1:
C1 =
0.25*Re-0.35
Where,
Geometry
correction, C3:
For segmented fin tubes arranged in, a
staggered pattern
C3 =
0.55+0.45*e(-0.35*lf/Sf)
an inline pattern,
C3 =
0.35+0.50*e(-0.35*lf/Sf)
For solid fin tubes
arranged in, a staggered pattern
C3 =
0.35+0.65*e(-0.25*lf/Sf)
an inline pattern
C3 =
0.20+0.65*e(-0.25*lf/Sf)
Where,
|
lf = Fin height, in |
|
sf = Fin spacing,
in |
Non-equilateral & row correction,
C5:
For fin tubes arranged in, a staggered pattern
C5 =
0.7+(0.70-0.8*e(-0.15*Nr^2))*e(-1.0*Pl/Pt)
an inline pattern
C5 =
1.1+(0.75-1.5*e(-0.70*Nr^2))*e(-2.0*Pl/Pt)
Where,
|
Nr = Number of tube rows |
|
Pl = Longitudinal tube pitch, in |
|
Pt = Transverse tube pitch,
in |
Mass Velocity, Gn:
Gn =
Wg/An
Where,
|
Wg = Mass gas flow, lb/hr |
|
An = Net free area,
ft2 |
Net Free Area,
An:
An = Ad - Ac *
Le * Nt
Where,
|
Ad = Cross sectional area of box, ft2 |
|
Ac = Fin tube cross sectional area/ft,
ft2/ft |
|
Le = Effective tube length, ft |
|
Nt = Number tubes wide |
|
And, |
|
Ad = Nt * Le * Pt /
12 |
|
Ac = (do + 2 * lf * tf *
nf) / 12 |
|
tf = fin thickness, in |
|
nf = number of fins,
fins/in |
Surface Area Calculations:
For
the prime tube,
Apo = Pi * do (1- nf *
tf) / 12
And for solid fins,
Ao = Pi*do(1-nf*
tf)/12+Pi*nf(2*lf(do+lf)+tf(do+2*lf))/12
And
for segmented fins,
Ao = Pi*do(1-nf*
tf)/12+0.4*Pi*nf(do+0.2)/12+Pi*nf
(do+0.2)((2*lf-0.4)(wn+tf)+ws*tf)/(12*ws)
And
then,
Afo = Ao -
Apo
Where,
|
ws = Width of fin segment, in |
We can
describe a sample fin tube bank as follows:
|
Process Conditions:
Gas flow, lb/hr = 100,000
Gas
temperature in, °F = 1000
Gas temperature out, °F = 591
Average fin
temperature, °F = 755
Compostion, moles
N2, % =
71.5779
O2, % = 2.8800
CO2, % =
8.6404
H2O, % = 16.4044
Ar, % = 0.8609
|
 |
|
Mechanical Conditions:
Tube Diameter, in = 4.500
Tube
Spacing, in = 8
Number Tubes Wide = 8
Tube Effective Length, ft =
13.000
Number Of Tubes = 48 |
Tube Arrangement = Staggered Pitch
Fin Height, in = 0.75
Fin
Thickness, in = 0.05
Fin Density, fins/in = 6
Fin Type =
Segmented
Fin Segment Width, in = 0.3125
|
Gas
Properties
For the gas properties, we can use the script we used in the
radiant section design to get the properties of the gas at the average
temperature. From
this program, we get the following properties,
kb, Btu/hr-ft-F =
0.0290
cp, Btu/lb-F = 0.2858
mb, cp = 0.0317 = 0.0317*2.42 = 0.0767
lb/hr-ft
To calculate the mass velocity, Gn, we need to first
calculate the net free area of the tube bank. For these calculations, we are
going to assume the tube rows are corbelled, so the net free area,
An:
Ad = 8*13*8/12 = 69.333
Ac =
(4.5+2*0.75*0.05*6)/12 = 0.4125 So,
An = 69.333 - 0.4125 * 13 * 8 = 26.4333
And,
Gn = 100000 / 26.4330 = 3783.1069
Now we can
calculate the reynolds number, Re,
Re = 3783.1069*4.5/(12*0.0767) = 18496.2854
And,
C1 = 0.25*18496.2854-0.35 =
0.0080
For,
sf = 1/6-.05=0.1167
C3 = 0.55+0.45*e(-0.35*0.75/0.1167) =
0.5975
And,
Pl =
(82-8/22)0.5=6.9282
C5 =
0.7+(0.70-0.8*e(-0.15*6^2))*e(-1.0*6.9282/8) =
0.9929
Now we can calculate the Colburn factor,
j =
0.0080*0.5975*0.9929(6/4.5)0.5((795.5+460)/(755+460))0.25
= 0.0055
And finally,
hc = 0.0055*3783.1069*0.2858 (0.0290
/(0.2858*0.0767))0.67 = 7.1732
To get a feel
for the values of the coeffcient, use the following script to run various
designs.
The radiation transfer coefficient, hr is described later in this
section. Fouling resistances, Rfi and Rfo are allowances
that depend upon the process or service of the heater and the fuels that are
being burned.
Fin Efficiency, E:
For segmented fins,
E = x * (0.9 + 0.1 * x)
And for solid fins,
E = y * (0.45 * ln(df / do) * (y - 1) +
1)
Where,
y = x * (0.7 + 0.3 * x)
And,
x = tanh(m * B) / (m * B)
Where,
B = lf + (tf /2)
For segmented fins,
m = (ho (tf + ws) / (6 * kf
* tf * ws))0.5
And for solid fins,
m = (ho / (6 * kf *
tf))0.5
Fin Tip Temperature,
Ts:
The average fin tip temperature is calculated as
follows,
Ts = Tg + (Tw - Tg) *
1/((e1.4142mB+e-1.4142mB)/2)
Maximum Fin
Tip Temperature, Tfm:
The maximum fin tip temperature is
calculated as follows,
Tsm = Twm + q(Tgm - Twm)
Where,
|
Tsm = Maximum Fin Tip Temperature, F |
|
Tgm = Maximum Gas Temperature, F |
|
Twm = Maximum Tube Wall Temperature,
F |
And, The value for theta, q, can be described by the following curve.
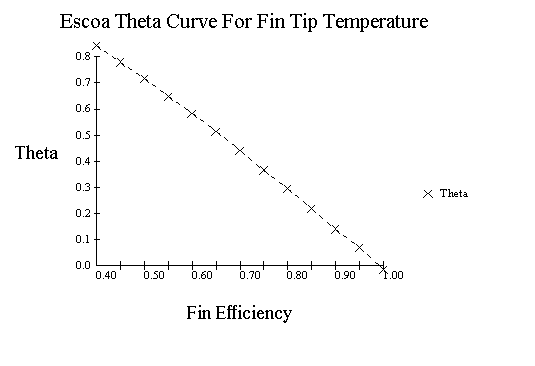
Convection Transfer, Stud Tubes
For
studded tubes, the correlations used are as provided by Birwelco,
Ltd.
Overall Heat Transfer Coefficient, Uo:
Uo =
1/Rto
Where,
|
Uo = Overall heat transfer coefficient,
Btu/hr-ft2-F |
|
Rto = Total outside thermal resistance,
hr-ft2-F/Btu |
And,
|
Rto = Ro + Rwo + Rio |
|
Ro = Outside thermal resistance,
hr-ft2-F/Btu |
|
Rwo = Tube wall thermal resistance,
hr-ft2-F/Btu |
|
Rio = Inside thermal resistance,
hr-ft2-F/Btu |
And the resistances are
computed as,
|
Ro = 1/he |
|
Rwo =
(tw/(12*kw))(Ao/Aw) |
|
Rio =
((1/hi)+Rfi)(Ao/Ai) |
Where,
|
he = Effective outside heat transfer coefficient,
Btu/hr-ft2-F |
|
hi = Inside film heat transfer coefficient,
Btu/hr-ft2-F |
|
tw = Tubewall thickness, in |
|
kw = Tube wall thermal conductivity, Btu/hr-ft-F |
|
Ao = Outside surface area, ft2/ft |
|
Aw = Mean area of tube wall, ft2/ft |
|
Ai = Inside tube surface area, ft2/ft |
|
Rfi = Inside fouling resistance,
hr-ft2-F/Btu |
Effective outside heat
transfer coefficient, he: For staggered and inline pitch,
he =
(hso*E*Afo+ht*Apo)/Ao
Where,
|
ht = Base tube outside heat transfer coefficient,
Btu/hr-ft2-F |
|
hso = Stud outside heat transfer coefficient,
Btu/hr-ft2-F |
|
Ao = Total outside surface area, ft2/ft |
|
Afo = Stud outside surface area, ft2/ft |
|
Apo = Tube outside surface area,
ft2/ft |
Inline pitch correction,
he =
he*(do/Pl)0.333
Where,
|
do = Outside tube diameter, in |
|
Pl = Longitudinal pitch of tubes,
in |
Base tube outside heat transfer coefficient,
ht:
ht =
(0.717/do0.333)(Gn/1000)0.67(Tb+460)0.3
And
the stud coefficient,
hs =
0.936*(Gn/1000)0.67(Tb+460)0.3
With
fouling,
hso =
1/(1/hs+Rfo)
Where,
|
hs = Stud outside heat transfer coefficient,
Btu/hr-ft2-F |
|
Gn = Mass velocity of flue gas, lb/hr-ft2 |
|
Tb = Average gas temperature, F |
Stud
efficiency, E:
E =
1/((ex+e-x)/1.950)
Where,
X =
Ls/12((2*hso)/(ks*Ds/12))0.5
And,
|
Ls = Length of stud, in |
|
Ds = Diameter of stud, in |
|
ks = Conductivity of stud,
Btu/hr-ft-F |
The following script will allow us
calculate the coeffcient for stud tubes.
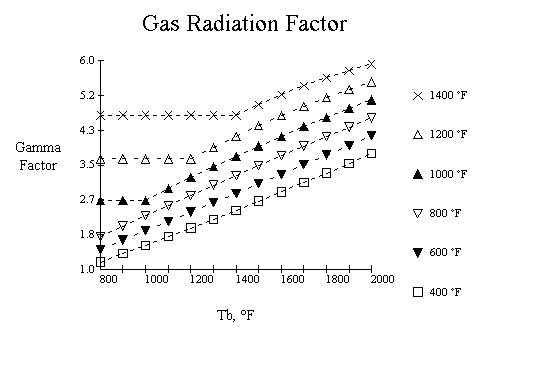
Short Beam, Reflective Radiation
The gas radiation factor, hr, can be calculated from the following
correlations. This factor is used in calculating the overall heat transfer
coefficient for bare tubes and fin tubes. The formulas for the stud tubes has
this factor built into the equations. For bare tubes,
hr = 2.2*gr*(pp*mbl)0.50
And
for fin tubes,
hr = 2.2*gr*(pp*mbl)0.50(Apo/Ao)0.75
Where,
|
hr = Average outside radiation heat transfer coefficient,
Btu/hr-ft2-F |
|
gr = Outside radiation factor,
Btu/hr-ft2-F |
|
pp = Partial pressure of CO2 & H2O, ,
atm |
|
mbl = Mean beam length, ft |
|
Apo = Bare tube exposed surface area,
ft2/ft |
|
Ao = Total outside surface area,
ft2 |
Outside radiation
factor, g r:
The outside radiation factor can be described by the following
curves:
»» جهت دریافت اطلاعات کامل در
مورد این مقاله و پکیج محاسبات حرارتی با شماره
تلفن 09126271381 تماس حاصل فرمایید.
|
|





