|
Based on article by Carl A. Vancini, in Chemical Engineering, March 22, 1982
Here a simple heat balance serves as the basis for calculating the flame temperature.
The increase in enthalpy between the unburned and burned mixtures is set equal to the heat produced by combustion.
Up to a flame temperature of about 2,500 °F, the burned mixture generally includes such ordinary gases as
CO2, N2, SO2, H2O, and residual O2 (from excess air).
At higher temperatures, CO2 appreciably dissociates to
CO and O2; H2O to O2 and OH-; O2 to O-2; H2 to H+
; N2 to N-3
and NO (produced by N2 and O2) to N-3 and O-2.
These dissociation reactions absorb an enormous amount of energy (heat), substantially lowering the flame temperature being calculated.
Heat Balance
The heat balance is calculated as follows: At constant pressure, the heat, Q, required to bring the temperature of
one pound of gas from temperature 0 to temperature t is:
The variation of cp with temperature can be approximated by a polynomial,
having the obvious advantage of being integrated easily. Using a third-degree
polynomial, we can write cp as:
|
cp = a + bt + ct2 + dt3
|
(2) |
where, a, b, c, and d are constants that depend on the nature of the gas. Equation (1) thus becomes:
|
Q = f0t (a + bt + ct2 + dt3
)dt
|
(3) |
Integrating:
|
Q = (a + bt/2 + ct2/3 + dt3/4)t
|
(4) |
It is customary to call the parenthetic term in Equation (4) the mean
specific heat:
|
Cmp = a + bt/2 + ct2/3 + dt3
/4
|
(5) |
So Equation 4 can be written as:
|
Cmpt = at + bt2/2 + ct2/3 + dt4
/4
|
(6) |
By taking mean specific heats instead of the true ones, we
can dispense with integration of Equation (1). Tabulations are available of cp
and cpm for many gases (not considering dissociation).
Dissociation
High-temperature dissociation of gases is a reaction that reaches equilibrium.
Equilibrium depends on composition, total pressure and temperature. The degree
of approach to equilibrium is also time-dependent. Tabulations of equilibrium
constants for common dissociation reactions are available.
Hand calculation of the effect of dissociation on the flame temperature is
extremely tedious, owing to the large number of reactions involved. For example,
in the combustion of acetylene with air, one must solve a set of ten equations
for ten unknown partial pressures. Here, polynomial expressions for the
equilibrium constants can be used [6], although with much difficulty.
Justi [7] gives values of the ratio nU/t (see nomenclature) for several
dissociation reactions at various temperatures at 1 atm. Assuming a linear
variation of the dissociation effects on temperature with the partial pressure
of each dissociating gas, the ratio nU/t can be used to modify the mean specific
heat of gases.
The figure illustrates the variation of cpm with temperature, for several gases.
This variation takes into account the above approach, which includes the effect
of dissociation. The profiles of cpm in this figure are somewhat different from
those calculated by applying the modifiers of Justi. Those in the figure use
more-recent thermal data and better values of calculated flame temperatures[8].
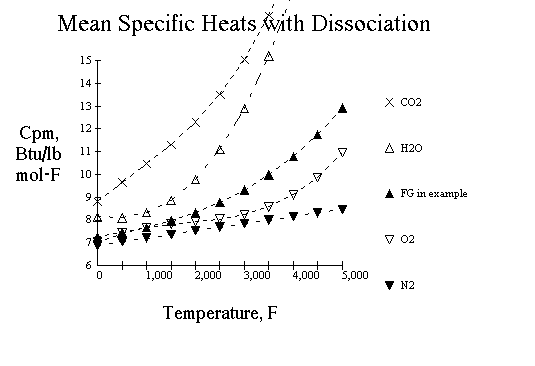
Limiting the maximum temperature to 5,000°F, a third-degree polynomial can be
fitted to the curves of cpm in the figure for CO2, H2O, and O2. For N2, which
dissociates appreciably only above 5,000 °F, a second-degree polynomial is
satisfactory. The coefficients are shown in Table II.
For transferring heat at a constant pressure:
|
Q = [a(t2-t1) + b/2(t2-t1)2
+ c/3(t2-t1)3 + d/4(t2-t1)
4]M |
(6) |
where Q is the heat produced by the fuel, M the amount of flue gas produced
per pound of fuel, and t1 and t2 the initial and final temperatures,
respectively.
M is also equal to the weight of fuel plus comburent (the substance that
supports combustion-e.g., air or oxygen). The initial temperature, t1, is that
of the fuel and comburent mixture.
The use of Equation (7) allows calculation of the flame temperature, t2, by
iteration via a programmable calculator. The result is not, however, to be taken
at face value, but rather for comparison. This is because the actual flame
temperature is always lower than the calculated one (by any method), for several
reasons:
1. There is radiation and conduction to the walls of the chamber in which
combustion takes place. Highly turbulent flames usually suffer an appreciable
heat loss.
2. Not all of the fuel is burned. Some part may remain with the ash(as the case
for solid fuels) or escape combustion in other ways.
3. The combustion space may be of such volume or geometry that there is not
enough time for all reactions of combustion and dissociation to reach
equilibrium.
In practice, the foregoing factors are usually compensted for by using an
empirical coefficient. it is multiplied by the heat of combustion that is
determined in the laboratory. Values of this coefficient are only estimates;
this is why the flame temperature calculated with any method can only
approximate actual values.
| Nomenclature |
| cp |
True specific heat, Btu/lb-°F |
| cpm |
Mean specific heat, Btu/lb-°F |
| n |
Fraction of gas dissociated |
| M |
Flue gas produced by one pound of fuel, lb/lb |
| Q |
Heat evolved by fuel during combustion, Btu/lb |
| t |
Temperature, °F |
| t1 |
Initial temperature of mixture fuel plus comburent, °F |
| t2 |
Temperature (average)of flame, °F |
| U |
Heat absorbed by dissociation reaction,
Btu/lb-mol |
| Empirical coefficients used in Equation (5).
Values account for dissociation |
Table II |
| Gas |
a |
b/2 |
c/3 |
d/4 |
| Carbon dioxide |
8.83 |
1.79 X 10-3 |
-2.63 X 10-7 |
1.19 X 10-10 |
| Oxygen |
7.04 |
1.0 X 10-3 |
-4.33 X 10-7 |
7.8 X 10-11 |
| Water vapor |
8.14 |
-3.1 X 10-4 |
4.3 X 10-7 |
8.7 X 10-11 |
| Nitrogen |
6.89 |
3.3 X 10-4 |
-3.0 X 10-9 |
|
| Range of validity: 0 to 5,000°F |
References:
1. Justi, E., and Luder, H., Furshung auf dem Gebide des Ingeniceruesiens,
Sept/Oct 1935, pp 210-211
2. Justi, E., Spezifische Warme, Enthalpie, Entropic and Dissoziation
technischer Gase, J. Springer Pub., Berlin, 1938, pp 143-151.
3. JANAF Thermochemical Tables, US Dept. of Commerce, Nat. Bur. of Standards,
NSRDS-NBS 27. 2nd ed., 1971.
4. Justi, E., op. cit. [2], pp 130-134.
5. Gaydon, A. G., and Wolfhard, H. G., Flames, Chapman and hall Pub., London,
1979, p. 334.
6. Protero, A., Combustion and Flame, Vol. 13, 1967, p. 399.
7. Justi, E., op. cit. [1], p. 215.
8. Gaydon, and Wolfhard, op. cit. [5], pp. 228 and 339.
9. Gas Engineers Handbook, McGraw-Hill Book Co., New York, 1934.
10. Johnson, A. J., and Auth, G. H., (eds), Fuels and Combustion Handbook,
McGraw-Hill Book Co., New York, 1950, p. 280.
11. Schnidman, I., (ed), Gaseous Fuel, American Gas Assn., New York, 1948.
»» جهت دریافت اطلاعات کامل در
مورد این مقاله و پکیج محاسبات حرارتی با شماره
تلفن 09126271381 تماس حاصل فرمایید.
|
|


