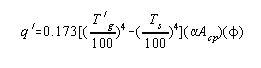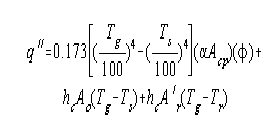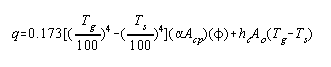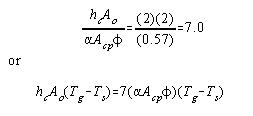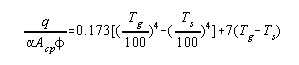|
GENERAL LIMITATIONS OF THE EMPIRICAL EQUATION
If a series of furnaces operate on fuels whose heating value varies
between comparatively narrow limits and whose ultimate
heat-receiving surface temperatures are nearly constant, the
performance of these furnaces may be adequately described by a
simple empirical equation. However, as conditions deviate from those
used to determine the constants of the equation its validity will be
questionable. For example, a valid equation determined for tubes at
a low temperature will certainly be invalid when the tube
temperature is increased to a much higher value because as this
temperature is increased it becomes more difficult to transfer a
given amount of heat in a given furnace. In other words, to maintain
a definite radiant rate in a furnace with a high tube temperature,
more fuel must be fired.
Another disadvantage of the empirical equation is the difficulty of
allowing for the effect of excess air unless a fuel of approximately
constant heating value is used. If, for example, an air-fuel ratio
is used to measure the effect of air addition, large values of the
ratio are commonly associated with high percentages of excess air
and low available heats. Conversely, small values of the ratio are
associated with low percentages of excess air and high available
heats. The danger involved in the indiscriminate use of an air-fuel
ratio is best illustrated by an example. For theoretical combustion
an average blast furnace gas would have an air-fuel ratio of
approximately 0.73 lbs. air per lb. fuel gas and a natural gas might
have a ratio of 15.9, yet the theoretical flame temperature of the
blast furnace gas would be only 2800° F. as compared to 3580° F. for
the natural gas. If the excess air in the case of the combustion of
the blast furnace gas were increased until the air-fuel ratio became
15.9, the theoretical flame temperature would drop to a temperature
much lower than 2800° F. If the the tube temperature was then
increased, a point would be reached where no heat could be
transferred to the tubes. However, with the same net heat
liberation, natural gas fuel would transfer a finite amount of heat.
Realizing the limitations of the purely empirical approach it was
decided to develop a theoretical radiant heat equation, simplified
by assumptions, if necessary, and to test it by the application to*
data obtained on furnace performance.
*It should be remembered, however, that in many furnaces the usual
measurement of the temperature of the gases leaving the radiant
section does not give Tg directly, but a value usually less than Tg
depending on the quantity of heat lost by the flue gases to the
convection section by radiation at the point of measurement.
DEVELOPMENT OF THE THEORETICAL RADIANT EQUATION
By a proper definition of terms the heat transferred in the radiant
section could be predicted exactly by a Stefan-Boltzmann type
equation.
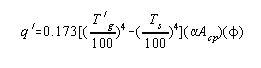 |
(8) |
q ' = net heat transferred by radiation to the tubes, B.t.u./hour
T 'g = mean temperature of the hot gases in the furnace, °F. + 460
T 's = mean tube skin temperature, °F. + 460.
aAcp = area of a plane
which will absorb the same as the actual cold surface in the
furnace, sq. ft.
f = an overall exchange factor correcting for flame emissivity,
arrangement of the refractory, volume of the combustion chamber,
etc. This factor will be discussed in detail later.
In the combustion chamber Tg° the mean
temperature of the hot gases in the furnace and the temperature of
the exit gases will undoubtedly differ, but run somewhat parallel.
However, it was assumed that T 'g could be replaced by the exit temperature,
Tg .* This assumed
interchangeability introduces, of course, a degree of empiricism
into the equation which will be justified, however, if the results
are satisfactory.
All the net heat transferred to all the surfaces in the radiant
section, i.e., the heat lost by the flame, is given by the following
equation:
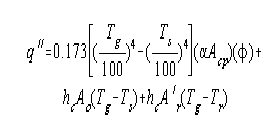 |
(9) |
A'r = area of refractory in furnace, sq. ft.
Ao = circumferential tube surface, sq. ft.
hc = convection coefficient, B.t.u./hour/sq.ft./°F.
Since both the external losses
from the furnace and the net heat transferred to the refractory by
convection, given by the term hcA'r(Tg-Tr), are usually small, the two may be
assumed equal without appreciably affecting the results.
Equation (9) may then be rewritten to give instead the heat
received by the oil:
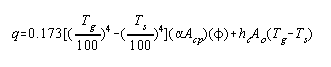 |
(10) |
The second term represents the heat transferred to the tubes
by convection and it may be approximated as its magnitude is
usually much smaller than the first term of equation (10).
By making the assumptions that:
1. The convection
coefficient lies normally between 2 and 3
B.t.u./hour/sq.ft./°F.;
2. In most furnaces Ao equals (2a Acp) approximately;
3. The overall exchange factor f has a value of about 0.57;
the terms hc and Ao in equation (10) can be expressed in
terms of a Acp and
f, thus:
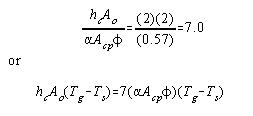 |
(11) |
Making this substitution in equation (10):
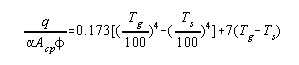 |
(12) |
Of the various ways that equation (12) representing the heat
transfer relation can be combined with the equation
representing a heat balance on the combustion chamber, the
following graphical procedure is suggested :
Let
H = the total net heat input to the furnace from all
sources; i.e., combustion of the fuel, sensible heat in the
air and fuel, sensible heat in recirculated flue gases,
etc., B.t.u./hr.
q = the total net heat absorbed in the radiant section by
the ultimate heat-receiving surface, B.t.u./hr.
N = the hourly heat capacity of the flue gas evaluated at
the temperature of the gasses leaving the section,
B.t.u./hr./°F. = (mols/hours) (mean MCp between
tg and
60°F.) (see Figure No. 15 in Appendix)
b = fraction of total net heat input lost from the external
furnace walls
tg = temperature of the gases leaving the section, °F.
bH = total heat losses, B.t.u./hr.
<-- page 2 -- page 4-->
|
|