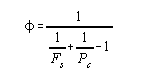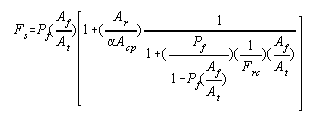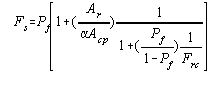|
EVALUATION OF THE EQUIVALENT
SURFACE, aAcp
Acp is the area of a continuous
plane replacing the row of tubes and may be taken as the product of
the exposed tube length, and center to center distance between
tubes, and the number of tubes in the exposed radiant row. a is the
ratio of reception by the actual surface to reception by a
continuous plane. Then the term aAcp is the tube area expressed as
equivalent cold plane surface, i.e., the area of a plane which will
absorb the same as the actual cold surface in the furnace.
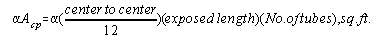
Hottel8 gives a as a
function of the ratio
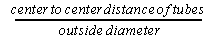
as in Figure 5.
| The following example illustrates the method of calculating
aAcp. |
| Assume a radiant section of the following characteristics
: |
|
Size of tubes |
5" outside diameter |
|
Center to center distance of tubes |
10" |
|
Exposed length of tube |
30 ft. |
|
Total number of tubes |
60 |
|
Arrangement of tubes, 2 rows on equilateral triangular
spacing |
|
Number of tubes per row |
30 |
|
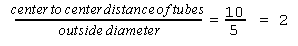 |
|
a=0.984, i.e., total
to 2 rows |
|
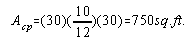 |
|
aAcp=0.984(750)=738 sq.ft. equivalent
cold plane surface. |
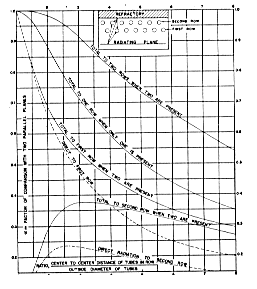 |
| Fig. 5 Distribution of Heat to One or Two Rows of Tubes
Mounted on |
| Refractory Wall and Irradiated from One
Side. |
Tubes on equalateral triangular centers; ordinate expressed on
basis of heat transfered from a plane to a plane replacing tubes, or
to infinite number of rows of tubes. These curves are a good
approximation for tubes placed on rectangular or square centers.
EVALUATION OF THE FLAME
EMISSIVITY, Pf
By definition, the emissivity of the flame is the ratio of the heat actually
transmitted from the flame to the cold surface to the heat which would have been
transmitted had the flame and the cold surface been perfect radiators. An
illustrative example of this calculation is available in the
literature.11
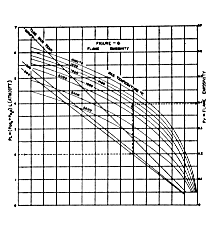
Figure No. 6 gives Pf in terms of
(PCO2+PH2O)L, tg, and
ts for cracked gas fuel and a tube emissivity of 0.90. This
plot is also a good approximation for fuel oil. The radiation cjharts of
Hottel9 which were used in this calculation are included in the
Appendix as Figures Nos. 13 and 14.
| PCO2 |
= |
partial pressure of carbon dioxide in the flue gas, atmospheres |
| PH2O |
= |
partial pressure of water vapor in the flue gas, atmospheres |
| L |
= |
mean length of radiant beam in the combustion chamber, feet |
| PL |
= |
atmospheres-feet |
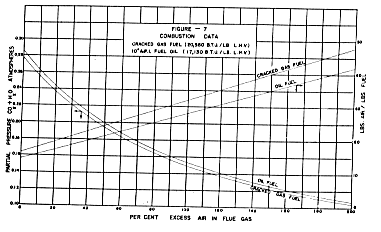
Values of PCO2 + PH2O and the air-fuel
ratio for typical cracked gas and oil fuels have been plotted on
Figure No. 7. The analysis of the fuels on which these calculations
are based are indicated in the Appendix.
MEAN LENGTH
OFRADIANT BEAMS
The mean length, L, of the radiant beam in the combustion chamber may
be estimated from Table I.
| Table I.-Mean Length of Radiant Beams in |
| Various Gas Shapes12 |
| From the values given by Hottel12
for the mean length, L, of radiant beams |
| in various gas shapes, the following
approximate values have been |
| derived for use in practical oil heater design.
These values |
| may be used until more exact methods are
available. |
| Dimensional Ratio |
|
| (length, width, height |
L |
| in any order) |
|
| Rectangular Furnaces |
|
| 1. |
1-1-1 |
to |
1-1-3 |
|
|
1-2-1 |
to |
1-2-4 |
2/3(Furnace Volume)1/3 |
| 2. |
1-1-4 |
to |
1-1-inf |
1 x smallest dimension |
| 3. |
1-2-5 |
to |
1-2-8 |
1.3 x smallest dimension |
| 4. |
1-3-3 |
to |
1-inf-inf |
1.8 x smallest dimension |
| Cylindrical Furnaces |
|
| 5. |
d x d |
|
|
2/3 x diameter |
| 6. |
d x 2d |
to |
d x inf |
1 x diameter |
EVALUATION OF THE
OVERALL ECHANGE
FACTOR, f
| Let |
|
|
| At |
= |
total area of furnace surfaces in the radiant section= |
|
|
Acp + refractory surfaces unprotected by tubes, sq.
ft |
| aAcp |
= |
equivalent cold plane surface, sq.ft. |
| Ar |
= |
effective refractory surface, sq.ft. (Ar =
At - aAcp) |
| Pc |
= |
emissivity of the ultimate heat-receiving surface, assumed |
|
|
=0.90 |
| Pf |
= |
emissivity of the flame. |
| Frc |
= |
fraction of all the radiation emitted from all the refractory |
|
|
in all directions, which, if not absorbed by the gas, |
|
|
would hit cold surface aAcp |
The overall exchange factor, f, as defined by
Hottel9, is then :
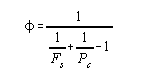 |
(18) |
Where
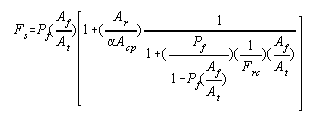 |
(19) |
Af = Area of the flame bundle, sq. ft.
In commercial
furnaces Af may be considered equal to At,
and equation (19) may be simplified to the form used in this study :
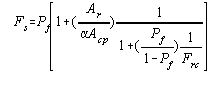 |
(20) |
The exact evaluation10 of Frc is rather tedious.
In an effort to simplify the evaluation of this factor, more than twenty
furnaces differing as widely as possible in design were studied, using the exact
technique referred to above. It was found that for ratios of
Ar/aAcp from 0 to
1, the value of Frc was adequately given by the ratio aAcp/At. For ratios of
Ar/aAcp from 3 to
6.5, Frc was very nearly equal to aAcp/Ar. Figure No. 8
embodies these results and gives f directly as a
function of the ratio Ar/aAcp and the flame emissivity
Pf.. Before discussing the results which prove the validity of the assumptions
made in the development of the radiant equation, a descriptive example will be
given to illustrate the use of the general method.
<-- page 4 (part1) --
page 2 -->
|
|